SOLUTION
We want to solve the question below
write an exponential equation in the form y = ab* whose graph passes through points (-3, 24) and (-2, 12).
Now an exponential equation is written in the form of
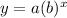
Now we will substitute -3 for x and 24 for y, we have

Also substituting -2 for x and 12 for y, we have

Dividing equation 2 by equation 1, we have

Now substitute this value of b into equation 2, we have

Substituting the values of a for 3 and b for 1/2, we have the equation as

Hence the last option is the answer