Question

Assuming that at t = 0 the message in a bottle is at its average height and moves upwards after, what is the equation of the function that could represent the situation?

Answer 1

Given that

The period is 24 seconds

The average height is 8 feet.

The distance between the maximum and minimum height is 4 feet.

Cosine function for this model.

At t=0 the function is in average height.

Let y be the height.

Let t be the time of seconds

The general cosine equation is

`y=a\cos (bt)+c`

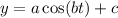
Here amplitude |a| represents the half distance between the maximum and minimum height.

`|a|=(4)/(2)=2`

`a=\pm2`

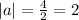
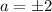
Substitute a=2 in the general equation, we get

`y=2\cos (bt)+c`
`\text{Period =}(2\pi)/(|b|)`

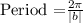
Substitute period =24, we get

`\text{24 =}(2\pi)/(|b|)`

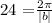
Using the cross product, we get

`24|b|=2\pi`

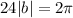
Dividing both sides by 24, we get

`|b|=(2\pi)/(24)=(\pi)/(12)`
`b=\pm(\pi)/(12)`

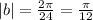
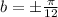
Substitute b=pi/12 in the general equation, we get

`y=2\cos ((\pi t)/(12))+c`

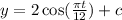
When t=0 the height is 8,

`8=2\cos ((\pi(0))/(12))+c`

`8=2(1)+c`
`c=8-2=6`
`c=6`

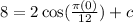
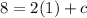
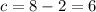
Substitute c=6 in the equation, we get

`y=2\cos ((\pi t)/(12))+6`

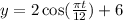
We get the equation for the average height, it will increase upward and reach the highest height.