Given:
Mean, μ = 95
Standard deviation, σ = 10
Let's find the test score 1.5 standard deviations below the mean.
To find the test score, apply the formula:
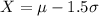
Thus, we have:
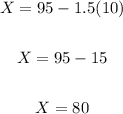
Therefore, the test score 1.5 standard deviations below the mean is 80 .
• ANSWER:
80