The system of equations describes three planes. If they intersect at one point then they have one solution; if they do not intersect, there are no solutions; If they overlap each other, then there are infinitely many solutions.
Let us solve the system.
Let us multiply the first equation by 2 and we get
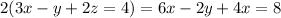
subtracting this from the second equation gives
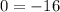
which implies no solutions. These two planes never intersect each other and it doesn't matter what the third plane does (because we want ALL THREE to intersect for a solution); therefore, this system does not have any solutions and hence we leave the blanks empty.