Question

Tony must find the distance from A to B on opposite sides of a lake. He located a point C that is 860 ft from A and 175ft from B. He measures the angle at C to be 78°. What is the distance from A to B?

Answer 1

We can solve this question using the next drawing to better see the situation:

Then, to find the distance AB, we can use the Law of Cosines, as follows:

`c^2=a^2+b^2-2a\cdot b\cdot\cos (C)`

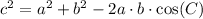
Then, we have that:

c = d = ?

a = 860 ft

b = 175 ft

cos(C) = cos(78)

Thus, applying the formula, we can substitute each of the value on it, as follows:

`c^2=860^2+175^2-2\cdot(860)\cdot(175)\cdot\cos (78)`

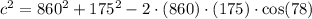
Then, we have:

`c^2=739600+30625-301000\cdot\cos (78)`
`c^2=707643.581064ft^2`

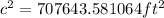
Thus

`\sqrt[]{c^2}=\sqrt[]{707643.581064ft^2}\Rightarrow c=841.215538ft`

Therefore, the distance from A to B (rounded to the nearest hundredth) is c = 841.22 ft.