Question

Which sequence of transformations maps figure one onto figure 2Figure one is mapped onto figure to by aA.) 90° clockwiseB.) 90° counterclockwiseC.) 180° clockwiseRotation about the origin followed by a translation ofA.) seven units rightB.) seven units leftC.) three units upD.) three units down

Answer 1

The transformation from figure 1 to figure 2 is shown on the graph.

It is required to choose from the options the composition of transformation that maps figure 1 onto figure 2.

The coordinates of the vertices of figure 1 are (5,2), (5,7), and (8,5).

The coordinates of the vertices of figure 2 are (-2,2), (-7,3), and (-5,5).

Recall the coordinate rule of 90º counterclockwise rotation about the origin:

`(x,y)\rightarrow(-y,x)`

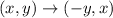
Hence, the rotation of figure 1 90º counterclockwise gives the vertices:

`(-2,5),(-7,5),(-5,8)`

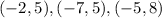
Translate the image 3 units down by subtracting 3 from the y-coordinates to give vertices:

`\begin{gathered} (-2,2),(-7,2),(-5,5) \\ \end{gathered}`

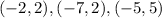
Notice that these vertices match that of figure 2.

It follows that the sequence of transformation is 90ºcounterclockwise rotation about the origin, followed by a translation three units down.

The answer is B followed by D.