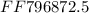Question

What is the mean of 40 100 25 90 85 95

Answer 1

Mean is also known as an average value amoung a set of data points, results, and tests.

Mathematically, mean ( average ) is defined as a weighted sum of data points. This can be expressed in a symbolic form as follows:

`\text{Mean = }\sum ^N_(n\mathop=1)((x_n)/(N))`

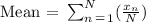
Where,

`\begin{gathered} x_n\colon\text{ The set of data points and type of data} \\ N\colon\text{ The total number of data-points} \end{gathered}`

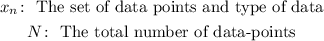
We are given with the following set of data points:

`x_1=40,x_2=100,x_3=25,x_4=90,x_5=85,x_6\text{ = 95}`

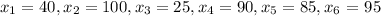
And we have a total of:

`N\text{ = 6 data points }`

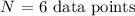
We will go ahead and plug in the respective values given into the formula for determining the mean value as follows:

`\text{Mean = }\frac{x_{1\text{ }}+x_2+x_3+x_4+x_5+x_6}{N}`

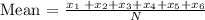
Plug in the respective data points as follows:

`\text{Mean = }\frac{40\text{ + 100 + 25 + 90 + 85 + 95}}{6}`

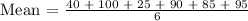
Evaluate as follows:

`\begin{gathered} \text{Mean = }(435)/(6) \\ \text{\textcolor{#FF7968}{Mean = }}\textcolor{#FF7968}{72.5} \end{gathered}`

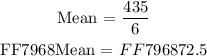
The mean ( average ) value for the given set of data points is:

`\textcolor{#FF7968}{72.5}`