Question

Given: Circle WW (-4, 6)Radius = 10 unitsWhich point lies on circle W?(0,4)(2, 10)(4,0)O , (6, 16)

Answer 1

A point will lies on the circle if the distance between the point and the center of the circle gives the radius or is equal to the radius.

Given the center of the circle

`(-4,6)`

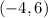
Let find the distance between the center and the point (4,0)

The formula for the distance between two points is given as

`\text{Distance}=\sqrt[]{(x_2-x_1)^2_{}+(y_2-y_1)^2_{}}`

Given the point (-4,6) and (4,0)

`x_1=-4,x_2=4,y_1=_{}6,y_2=0`

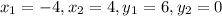
Then substitute the value above into the formula, we have

`\begin{gathered} \text{Distance}=\sqrt[]{(4-(-4)^2+(0-6)^2} \\ \text{Distance =}\sqrt[]{8^2_{}+(-6)^2} \\ \text{Distance}=\sqrt[]{64+36} \\ \text{Distance}=\sqrt[]{100} \\ \text{Distance}=10\text{units} \end{gathered}`

Since the distance is equal to the radius of the circle,

Hence the point (4,0) lies on the circle