First, find the surface area of each figure and then add their surface areas.
Notice that the figure is formed by two rectangular prisms. Each one, has 6 sides and each side is a rectangle. There are three pairs of equal sides on each prism: top-bottom, left-right and front-back faces.
Pink figure:
The top-bottom faces are rectangles of sides 5cm and 6cm. Then, the area of that pair of faces is:
![5\operatorname{cm}*6\operatorname{cm}=30cm^2]()
The front-back faces are rectangles of sides 5cm and 20cm. Then, the area of that pair of faces is:
![5\operatorname{cm}*20\operatorname{cm}=100cm^2]()
The left-right faces are rectangles of sides 20cm and 6cm. Then, the area of that pair of faces, is:
![20\operatorname{cm}*6\operatorname{cm}=120cm^2]()
To find the surface area of the prism, add the area of each type of side twice:
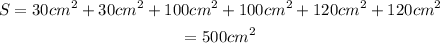
Purple figure
Do the same procedure, but notice that the dimentions of the prism are not the same.
Top-Bottom: 4cm x 6cm = 24cm^2
Left-right: 12cm x 6cm =72cm^2
Front-back: 4cm x 12 cm = 48cm^2
Then, the surface area of this prism is:
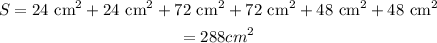
Finally, to find the surface area of both figures together, add their surfaces:

Therefore, the surface area of the composite figure, is:
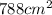
BEWARE:
Notice that there is a region where both boxes are in contact. That surface may not account to the total surface area if both boxes are fused together. In that case, notice that the area corresponds to the left-right side of the purple prism. Then, we should substract twice that area from the past result to find the surface area of both fused together prisms.
That area was equal to 72 cm^2. Then, the total area would actually be:
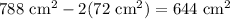
So, the total area of both fused together prisms, is:
