1) Since this is a Conditional Probability, we can write out the following formula for that:
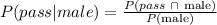
2) Now, in the table we can see that the subspace for those who passed is the sum of all who passed:
28 +12 = 40
The Subspace for the students is:
21 +49 = 70
And now we can plug into that formula checking in the table:
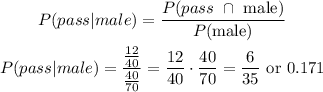
2.2) The Probability of being approved:
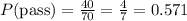
We can check whether two events are independent if we can state that
![undefined]()