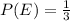Question

A student has a one-dollar bill, a five-dollar bill, and a ten-dollar bill in a box. The student selects a bill from the box 44 times and selects the 10-dollar bill 15 times. What formula should be used to calculate the experimental probability? What is the experimental probability of selecting the 10 dollar bill? What is the theoretical probability of selecting the 10 dollar bill?

Answer 1

Experimental Probability:

- The experimental probability is the probability gotten from performing an experiment.

- The formula for finding the experimental probability is similar to theoretical probability, only that it only takes the values of the experiment into consideration. That is,

`\begin{gathered} ProbabilityofanEventP\left(E\right)=Numberoftimesaneventoccurs \\ P(E)=\frac{Number\text{ of times Event E occurred}}{Number\text{ of trials}} \end{gathered}`

- In this case, the Event (E) is the event when the student picks the $10 bill. The question tells us the number of times the student selected the $10 bill is 15 out of a total number of trials of 44.

- Thus, we can find the Experimental Probability P(E) as follows:

`P(E)=(15)/(44)`

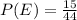
Theoretical Probability:

- The theoretical probability does not need the values from an experiment. We only consider the hypothetical situation of choosing a particular dollar bill.

- We have 3 bills; $1, $5, and $10. This means that if we are to choose 1 of the bills, the chances of us actually picking one of them is

`(1)/(3)`

- This represents the theoretical probability of choosing any of the 3 bills. It is the same for the 3 bills because we have just 1 of each bill in the box and as a result, there should be no reason why one bill should have a greater chance of being selected.

- Thus, the theoretical probability of choosing the $10 bill is

`P(E)=(1)/(3)`