Question

Consider the circuit drawn below. Find the values of each of the currents.

Answer 1

We are asked to determine the values of the currents.

Since the 4 Ohms resistance is parallel to the 12v voltage source this means that the voltage through this resistance is also 12 V. We can determine the current using Ohm's law:

`I_2=(V)/(R_2)`

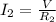
Now, we plug in the values:

`I_2=(12V)/(4\Omega)`

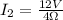
Solving the operations:

`I_2=3A`

Now, since the 6 Ohms and 8 Ohms resistors are also parallel to the voltage source, the voltage through these resistors is 12V. We can determine the current also using Ohm's law:

`I_3=(V)/(R_3)`

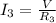
The resistance is the equivalent resistance. Since the resistors are connected in parallel this means that the total resistance is the sum of both resistances:

`R_3=6\Omega+8\Omega=14\Omega`

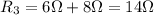
Now, we substitute and we get:

`I_3=(12V)/(14\Omega)=0.86A`

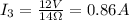
Now, currents 3 and 2 add up to current 1, therefore:

`I_1=I_2+I_3`

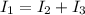
Substituting the values:

`I_1=3A+0.86A=3.86A`

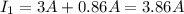
Therefore, the current 1 is 3.86 Amperes.