Question

Find the vertex for the parabola whose equation is given by writing the equation in the form y = ax² +bx+c.y=(x-3)²-5***(Type an ordered pair.)The vertex is

Answer 1

Given: A parabola equation

`y=(x-3)^2-5`

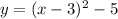
Required: To find the vertex of the given parabola.

Explanation: The given equation can be written as

`\begin{gathered} y=x^2+9-6x-5 \\ y=x^2-6x+4 \end{gathered}`

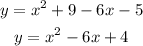
Now the general equation is of the form

`y=ax^2+bx+c`

Comparing both equations we get,

`\begin{gathered} a=1 \\ b=-6 \\ c=4 \end{gathered}`

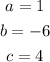
The x-coordinate of the vertex is

`\begin{gathered} x=-(b)/(2a) \\ x=(-(-6))/(2(1)) \\ x=3 \end{gathered}`

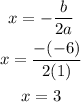
For the y coordinate of the vertex, put x=-3 in the equation of parabola

`\begin{gathered} y=(3)^2-6(3)+4 \\ y=-5 \end{gathered}`

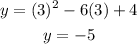
Hence the coordinate of the vertex is (-3,31)

Final Answer: The vertex is (3,-5).