Question

The distance between the centers of two planets is 5 x 10^10 km, if the planets move and the distance changes to 2 x 10^10 km, what would happen to the gravitational force between the planets? Decrease or Increase. Explain

Answer 1

Given:

Original distance between the planets, d1 = 5 x 10¹⁰ km

Distance after the planets moved, d2 = 2 x 10¹⁰ km.

Let's determine what would happpen to the gravitational force between the planets.

Apply the formula:

`F=G(m_1m_2)/(d^2)`

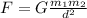
Let F1 be the gravitational force before the movement.

Let F2 be the gravitational force after the movement.

`\begin{gathered} F_1=(Gm_1m_2)/(d^2_1) \\ \\ F_2=(Gm_1m_2)/(d^2_2) \end{gathered}`

Equate both equations

Now, for the two gravitational forces, we have the equations:

`\begin{gathered} F_1=(Gm_1m_2)/((5*10^(10))^2) \\ \\ F_2=(Gm_1m_2)/(2*10^(10)) \end{gathered}`

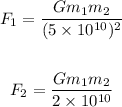
The relationship between the gravitational force between planets and the distance is:

`F=(1)/(r^2)`

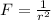
The gravitational force is inversely proportional to the square of the distance between the planets.

Thus, we have:

`\begin{gathered} F_1=(1)/((5*10^(10)))=4*10^(-22)\text{ N} \\ \\ F_2=(1)/((2*10^(10))^2)=2.5*10^(-21)N \end{gathered}`

We can see the force after the movement F2 is greater than the force before the movement F1.

Therefore, the gravitational force will increase.

ANSWER:

Increase.