Question

System of equationsstruggling terribly and teacher is vague with questions please help

Answer 1

We have the system of equations:

`\begin{gathered} 3x+2y=16 \\ 3y=-2x-10 \end{gathered}`

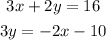
We can use the substitution method to solve it.

We select one variable and clear its value in function of the other. For example we take the second equation and calculate the value of y in function of :

`\begin{gathered} 3y=-2x-10 \\ y=(-2x-10)/(3) \end{gathered}`

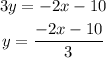
Then, we replace the expression for y in the other equation and solve for x:

`\begin{gathered} 3x+2y=16 \\ 3x+2((-2x-10)/(3))=16 \\ 3x-(4)/(3)x-(20)/(3)=16 \\ 3(3x-(4)/(3)x-(20)/(3))=3\cdot16 \\ 9x-4x-20=48 \\ 5x=48+20 \\ 5x=68 \\ x=(68)/(5)=13.6 \end{gathered}`

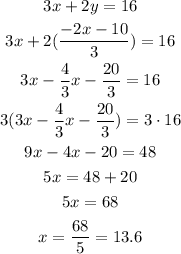
Then, if we calculate the value for y we get:

`y=(-2x-10)/(3)=(-2(13.6)-10)/(3)=(-27.2-10)/(3)=(-37.2)/(3)=-12.4`

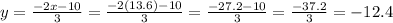
The solution for this system is (x,y)=(13.6, -12.4).

NOTE: if what we want is to verify if a certain pair (x,y) is a solution to the system of equations, we replace the values of x and y in the equations and see if the equations verify.

For a certain pair to be the solution to the system, it has to verify both equations.

For example, if we want to test if (-6,1) is the solution for the system, we replace the values of x and y in the first equation:

`\begin{gathered} 3(-6)+2(1)=16 \\ -18+2=16 \\ -16\\eq16\longrightarrow\text{ does not verify (is not a solution) } \end{gathered}`

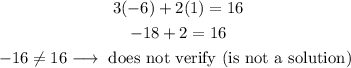
As it does not verify one of the equations, we already know that (-6,1) is not a solution to the system of equations.