Question

Henry's Coffee Shop makes a blend that is a mixture of two types of coffee. Type A coffee costs Henry 4.05 per pound, and type B coffee costs $5.80 per pound. This month, Henry made 124 pounds of the blend, for a total cost of 622.95. How many pounds of type B coffee did he use?

Answer 1

Step-by-step explanation:

Given;

We are told that Henry makes a mix of type A and type B coffee. Also he made a total of 124 pounds and that cost a total of $622.95, meanwhile one pound of type A costs $4.05 and one pound of type B costs $5.80.

Required;

We are required to calculate how many pounds of type B was used in the mixture.

Step-by-step solution;

To solve this problem we shall begin by assigning variables to the unknown quantities. We shall call type A coffee x, and type B coffee shall be y.

If Henry made a total of 124 pounds of the coffee blend, then we will have the following equation;

`x+y=124-----(1)`

Also type A costs $4.05 and type B costs $5.80. If the mixture of both costs $622.95, then we can represent this by the following equation;

`4.05x+5.80y=622.95-----(2)`

We can now solve the system of equations for x (type A) and y (type B).

We shall start with equation (1), make x the subject of the equation;

`x=124-y`

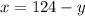
Next we substitute the value of x into equation (2);

`\begin{gathered} 4.05x+5.80y=622.95 \\ \\ 4.05(124-y)+5.80y=622.95 \\ 502.2-4.05y+5.80y=622.95 \end{gathered}`
`\begin{gathered} 5.80y-4.05y=622.95-502.2 \\ \\ 1.75y=120.75 \end{gathered}`

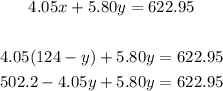
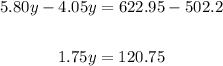
We now divide both sides by 1.75;

`\begin{gathered} (1.75y)/(1.75)=(120.75)/(1.75) \\ \\ y=69 \end{gathered}`

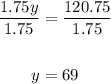
We can now substitute the value of y back into equation (1);

`\begin{gathered} x+y=124 \\ x+69=124 \\ x=124-69 \\ x=55 \end{gathered}`

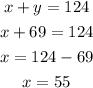
Therefore, Henry used 55 pounds of type A coffee and 69 pounds of type B coffee.

ANSWER:

Type B coffee was 6