We will have the following:
First, we remember that suplementary angles add to 180°; knowing this, we can see that the supplementary angle for
We also remember that the sum of internal angles of a triangle also add to 180°, so the following is true:
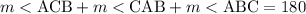
So:
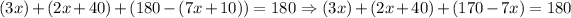
Now, we solve for x, that is:
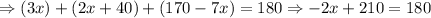
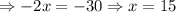
Now, knowing this we will find the measure of angle ABC, that is:
[tex]m<\text{ABC}=170-7x\Rightarrow mSo,
the measure of the angle ABC is 65°.