Question

Find all global maxima and minima values for the function y = x^2 + 54/x on the interval [1, 108).Global Maximum:Global Minimum:

Answer 1

Given the equation:

`y=x^2+(54)/(x)`

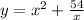
Let's find the global maxima and minima values for the function on the interval [1, 108]

To find the global maxima on the interval, let's first find the derivative:

`y^(\prime)=2x-(54)/(x^2)`

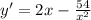
Set the derivative to zero and solve for x:

`\begin{gathered} 2x-(54)/(x^2)=0 \\ \\ (2x\left(x^2\right)-54)/(x^2)=0 \\ \\ 2x^3-54=0 \end{gathered}`

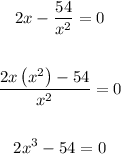
Add 54 to both sides:

`\begin{gathered} 2x^3-54+54=0+54 \\ \\ 2x^3=54 \\ \\ x^3=(54)/(2) \\ \\ x^3=27 \\ \\ Take\text{ the cuberoot of both sides:} \\ \sqrt[3]{x^3}=\sqrt[3]{27} \\ \\ x=3 \end{gathered}`

Substitute 3 for x in the original function and solve for y:

`\begin{gathered} y=x^2+(54)/(x) \\ \\ y=3^2+(54)/(3) \\ \\ y=9+18 \\ \\ y=27 \end{gathered}`

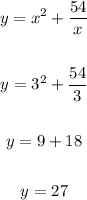
Therefore, the global minima is: (3, 27)

To find the global maxima, solve for the following:

at x = 1 and at x = 108

`\begin{gathered} y=1^2+(54)/(1)=54 \\ \\ \\ y=108^2+(54)/(108)=11664+0.5=11664.5 \\ \end{gathered}`

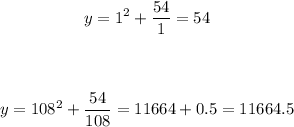
Therefore, the global maxima is: (108, 11664.5)

ANSWER:

Global maximum: (108, 11664.5)

Global minimum: (3, 27)