Question

A string of a given length and diameter and density is under a tension of 100 N and produces a sound of 200 Hz. How many vibrations per second will be produced if the tension is changed to :A. 900 NB. 25 N

Answer 1

Given,

The length, diameter, and density are given, i.e., the length, diameter and density of the string are constant.

The tension on the string, T₁=100 N

The frequency of the sound, f₁=200 Hz

The tension on the string and the frequency of the sound is related as,

`T=4ml^2f^2`

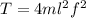
Where m is the mass of the string and l is the length of the string.

On rearranging the above equation,

`(T)/(f)=4ml^2`

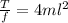
As the length, diameter, and density of the string is constant,

`\begin{gathered} (T)/(f)=\text{constant} \\ (T_1)/(f_1)=(T_2)/(f_2) \end{gathered}`

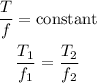
A.

Given,

Tension in the string, T₂=900 N

The frequency of the string after the change in the tension is given by,

`\begin{gathered} (T_1)/(f_1)=(T_2)/(f_2) \\ \Rightarrow f_2=(T_2* f_1)/(T_1) \end{gathered}`

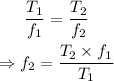
On substituting the known values,

`\begin{gathered} f_2=(900*200)/(100) \\ =1800\text{ Hz} \end{gathered}`

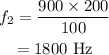
Thus the frequency of the sound after the tension on the string changes to 900 N is 1800 Hz, i.e., 1800 vibrations are produced per second.

B.

Given,

The tension on the string, T₃=25 N

The frequency of the string after the tension changes to 25 N is given by,

`\begin{gathered} (T_1)/(f_1)=(T_3)/(f_3)_{} \\ \Rightarrow f_3=(T_3* f_1)/(T_1) \end{gathered}`

On substituting the known values,

`\begin{gathered} f_3=\frac{25*200_{}}{100} \\ =50\text{ Hz} \end{gathered}`

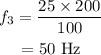
Thus the frequency of the sound after the tension changes to 25 N is 50 Hz, i.e., 50 vibrations are produced per second.