Question

17. The circle in the figure below has center o, which of the following measures for the figure would be sufficient by itself to determine the radius of the circle? I. The length of arc PQRII. The perimeter of A OPRIII. The length of chord PRA. NoneB. I onlyC. II onlyD. I and III

Answer 1

Given:

A circle is given with center O.

The objective is to choose the required measure to determine the radius of the circle.

Step-by-step explanation:

The given options are,

The length of the arc PQR,

The perimeter of ∆OPR,

The length of the chord PR.

From the figure, the angle formed by the sector is 90°.

The general formula for arc length (L) is,

`\begin{gathered} L=(\theta)/(360)*2\pi r \\ r=(L*360)/(\theta*2\pi) \end{gathered}`

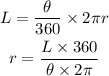
Here, if length of the arc and angle are substituted in the above formula, the radius of circle can be calculated.

Hence, radius of the circle can be calculated.

Considering the second option, if all the three sides of the triangle are unknown, the radius of the triangle cannot be calculated with the help of given perimeter.

Consider radius of circle as r and the chord as x.

`\begin{gathered} P=r+r+x \\ P=2r+x \\ 2r=P-x \\ r=(P-x)/(2) \end{gathered}`

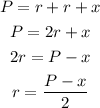
Here, if perimeter is given the length x is still unknown.

Hence, radius of the circle cannot be calculated.

If the length of the chord (x) is given for the isosceles right triangle, the two equal sides (r) can be calculated using Pythagorean theorem.

`\begin{gathered} r^2+r^2=x^2 \\ 2r^2=x^2 \\ r=\sqrt[]{(x^2)/(2)} \end{gathered}`

Here, by substituting the length of the chord, the radius of the circle can be calculated.

Thus, the radius of the circle can be calculated using either the arc length of the cirlcle or the length of the chord.

Hence, option (D) is the correct answer.