Question

Find the surface area using the net. HELP this is really confusing I need the steps if possible :(

Answer 1

We are asked to determine the surface area of the given pyramid. To do that we will add the areas of each of its faces. The front faces are triangles and their area is given by:

`A_f=(bh)/(2)`

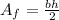
Where "b" is the base and "h" is the height. Replacing the known values:

`A_f=((5)(12))/(2)=30`

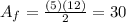
Since there are 4 faces, we will multiply this number by four when determining the total surface area. The bottom face is a square and its area is given by:

`A_b=l^2`

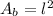
Where "l" is the length of its sides. Replacing the values:

`\begin{gathered} A_b=5^2 \\ A_b=25 \end{gathered}`

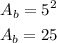
The total surface area is:

`A=4A_f+A_b`

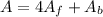
Replacing the values:

`\begin{gathered} A=4(30)+25 \\ A=120+25 \\ A=145 \end{gathered}`

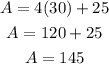
Therefore, the total surface area is 145 square units.