Answer:
Area of 1st sign is 50/3 ft^2.
Area of 2nd sign is 57/4 ft^2.
Area of the 1st sign is larger than that of the 2nd sign.
Step-by-step explanation:
To find the area of the 1st sign, we have to multiply the length and width of the sign given;
Let the area of the 1st sign be A1;
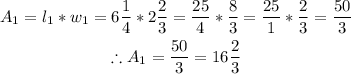
Therefore, the area of the 1st sign is 50/3 ft^2
Let the area of the second sign be A2;
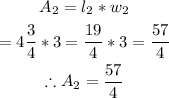
Therefore, the area of the 2nd sign is 57/4 ft^2.
To determine which fraction is greater, we have to make them both have a common denominator by multiplying the numerator and denominator of A1 by 4 and that of A2 by 3;
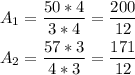
Since the numerator of A1 is greater than that of A2, it means that A1 is the largest.