Question

Find the value of 2 in the isosceles triangle shown below.5Сл306

Answer 1

Since we have an isosceles triangle, the segment x bisects the base of the triangle in two equal sides, forming two rectangle triangles on both sides of segment x. With rectangle triangles we can use the Pythagorean theorem, like this:

`h^2=a^2+b^2`

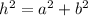
Where h is the hypotenuse of the triangle, a and b are its two legs.

In this case, the base of the isosceles triangle equals 6, then when we form the two internal rectangle triangles we get two sides with length 3, the hypotenuse of these triangles equals 5, then, by replacing these values into the above formula, we get:

`5^2=3^2+x^2`

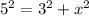
Solving for x, we get:

`\begin{gathered} 25=9+x^2 \\ 25-9=x^2 \\ 16=x^2 \\ \sqrt[]{16}=x \\ x=\sqrt[]{16}=4 \end{gathered}`

Then, x equals 4