Given:
The equation of a line is x-6y-5 = 0.
Another line passes perpendicular to the first line through the point (8, -8).
The objective is to find the equation of the second line in point slope form and general form.
Step-by-step explanation:
The general equation of line is,
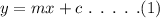
Here, m represents the slope of the line.
To find slope of first line:
The given equation of line 1 can be rewritten as,
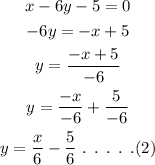
By comparing the equation (2) with the equation (1), the slope of the first line is,
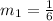
To find slope of line 2:
The slope of line 2 which is perpendicular to line 1 can be calculated as,
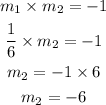
To find equation of line in point slope form:
The general formula of point slope form is,
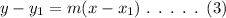
Consider the given coordinate as,
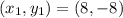
Substitute the value of coordinate and the slope in equation (3),
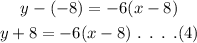
To find equation of line in general form:
The general formula of general form is,
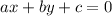
Then, equation (4) can be rewritten as,
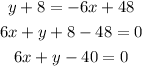
Hence,
The equation of line in point slope form is y +8 = -6(x-8).
The equation of line in general form is 6x + y -40 = 0.