1 Answer

Ask a Question

Sander Bollen · Answer 1 · 2023-02-28T06:29:32+0000

We are given the following data set

65 , 90, 85, 70, 70, 95, 55

The mean absolute deviation is given by

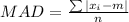
$MAD=(\sum|x_i-m|)/(n)$

Where xi is the individual values in the data set, m is the average value of the data set, and n is the number values in the data set.

The average value of the data set is given by

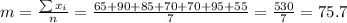
$m=(\sum x_i)/(n)=(65+90+85+70+70+95+55)/(7)=(530)/(7)=75.7$

So, the mean absolute deviation is

$\begin{gathered} MAD=(\sum|x_i-m|)/(n)=(|65-75.7|+|90-75.7|+|85-75.7|+|70-75.7|+|70-75.7|+|95-75.7|+|55-75.7|)/(7) \\ MAD=(|-10.7|+|14.3|+|9.3|+|-5.7|+|-5.7|+|19.3|+|-20.7|)/(7) \\ MAD=(10.7+14.3+9.3+5.7+5.7+19.3+20.7)/(7) \\ MAD=(85.7)/(7) \\ MAD=12.24 \end{gathered}$

Therefore, the mean absolute deviation for the given data set is 12.24

Option a is the correct answer.

0 Comments

Please log in or register to add a comment.

Please log in or register to answer this question.

1 Answer

0 Comments

Please log in or register to add a comment.

Other Questions