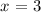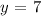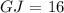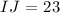Question:
Solution:
According to the figure, we have that:
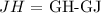
that is:
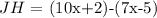
this is equivalent to:
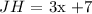
now, the diagonals of a parallelogram bisect each other. So that, we get the following equation:
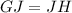
this is equivalent to:
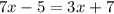
this is equivalent to:
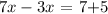
this is equivalent to:
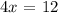
solving for x, we get:
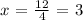
On the other hand, remember again that the diagonals of a parallelogram bisect each other. So that, we get the following equation:
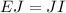
this is equivalent that
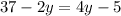
this is equivalent to:
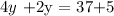
this is equivalent to:
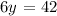
solving for y, we get:
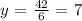
now, applying the values obtained for x and y we get:
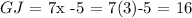
and
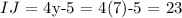
we can conclude that the correct answer is: