To find how many seconds will it be until the lights flicker together again we have to find the lowest common multiple LCM of the times each light flickers.
Since one of them flickers every 7 seconds, and 7 is a prime number (it can only be divided by 7 and 1) and the other light flickers every 8 seconds and 8 is not a multiple of 7, then the LCM in this problem is the multiplication between these two numbers:
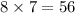
The lights will flicker again in 56 seconds