We are given the following equation
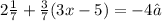
Let us first convert the mixed number (2 1/7) to a simple fraction
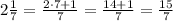
So the equation becomes
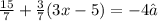
Now multiply the fraction 3/7 by the terms in the bracket
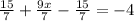
As you can see the fractions 15/7 cancels out.
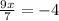
Finally, solving for x
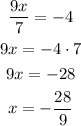
Therefore, the value of x is -28/9