Question

Simplify1. 6√802. 7√3 + 10√1083. 3/√7 W/ steps

Answer 1

We will simplify some radical numbers.

The firsts number to simplify is

`6√(80)`

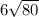
To simplify this number we have to factorize the number 80 that is inside the symbol square root, let us factorize 80

We conclude that 80 is equal to multiply four times 2 and once 5. Substituting 80 by its factorization we find

`6√(80)=6√(2^4\cdot5)`

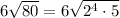
Now we will use the property of the radicals, that is that we can split the square into factors, as follows

`6√(80)=6√(2^4)√(5)`

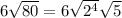
Now, we realize that four times two is 16, and the square root of 16 is 4, then we find that

`6√(80)=6\cdot4\cdot√(5)=24√(5)`

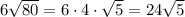
And this is the greater simplification that can be done for this number.

Now we will simplify the second number.

The second number is

`7√(3)+10√(108)`

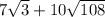
The number 3, is a prime number, so the first term is already simplified, we will simplify the second term, note that we factorize the number 108 as

`108=2^2\cdot3^3`

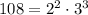
Therefore, writing the original number,we find

`7√(3)+10√(108)=7√(3)+10√(2^2)√(3^2)√(3)`

Where we have again applied the property of distribution of the square root over the factor, as the square root of 4 is 2, and of 9 is 3, we find

`\begin{gathered} 7√(3)+10√(108)=7√(3)+10\cdot3\cdot2√(3) \\ \\ =7√(3)+60√(3) \\ \\ =67√(3) \end{gathered}`

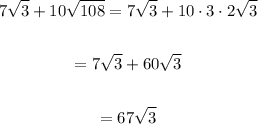
where in the last line we have used the common factor square root of three to sum the two terms.

The third number is

`(3)/(√(7))`

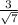
Simplify a number that have a radical in its denominator, is performed multiplying by 1, as follows

`(3)/(√(7))=(3)/(√(7))\cdot1=(3)/(√(7))\cdot(√(7))/(√(7))=(3√(7))/(√(7^2))=(3√(7))/(7)`

Where in the process we eliminate the square root from the denominator, the last number on the right is the simplification required