Question

A 62 kg swimmer pushes off from the wall at swim practice. If they are in contact with the wall for 0.24 seconds and the wall exerts a force if 662N on the swimmer when they push off, how fast are they moving after they push off if they start from rest?

Answer 1

2.56 m/s

Step-by-step explanation:

The change in the momentum is equal to the force times time. So, we have the following equation

`\begin{gathered} \Delta p=Ft \\ mv_f-mv_i=Ft \end{gathered}`

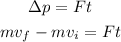
Where m is the mass, vf is the final velocity, vi is the initial velocity, F is the force and t is the time. Solving for vf, we get:

`\begin{gathered} mv_f=Ft+mv_i \\ \\ v_f=(Ft+mv_i)/(m) \end{gathered}`

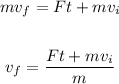
Now, we can replace F = 662N, t = 0.24 s, m = 62 kg, and vi = 0 m/s.

Then, the final velocity is

`\begin{gathered} v_f=\frac{(662N)(0.24s)+(62\text{ kg\rparen\lparen0 m/s\rparen}}{62\text{ kg}} \\ \\ v_f=2.56\text{ m/s} \end{gathered}`

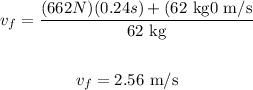
Therefore, the answer is 2.56 m/s