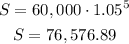The Graph of a Function
The formula:
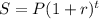
Will be used to calculating the future value of two conditions a and b
a) P = $60,000, r = 5% = 0.05, 0 ≤ t ≤ 12.
Substitute some selected values of t in the given interval.
For t=0:
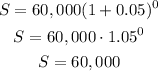
For t=3:
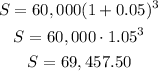
For t=6:
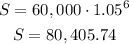
For t=9:
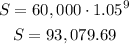
For t=12:
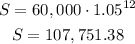
The graph that looks closer to the graph above is B.
b. Calculate the future value for t=5 years.