Question

I need help and I don’t understand if u can explain and guide me thru it?

Answer 1

The first figure has 10 small blocks

The second figure has 14 small blocks

Then the difference between the two figures is 14 - 10 = 4

Then it is an arithmatic sequance

a)

Then the next two figures will have (14 + 4 = 18 small blocks) and (18 + 4 = 22 small blocks)

You can draw them 18 = 9 x 2 and 22 = 11 x 2 small blocks

b)

The input will be the number of the figure (n)

The output is the number of the small blocks in each figure

Input: Output

1 10

2. 14

3. 18

4. 22

c)

The recursive formula of the arithmetic sequence is

`a1=1^(st)term,a_n=a_(n-1)+d`

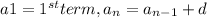
a1 is the first term

an is any term in the sequence

d is the difference between each 2 consecutive terms

Since a1 = 10

Since d = 4

Then the recursive formula is

`a_1=10,a_n=a_(n-1)+4`

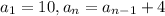
The explicit formula of the arithmetic sequence is

`a_n=a_1+(n-1)d`

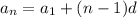
Since a1 = 10

Since d = 4

Then the explicit formula is

`a_n=10+(n-1)(4)`

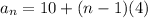
We will simplify it by multiplying the bracket by 4, then add the like terms

`\begin{gathered} a_n=10+(n)(4)-(1)(n) \\ a_n=10+4n-4 \\ a_n=(10-4)+4n \\ a_n=6+4n \end{gathered}`

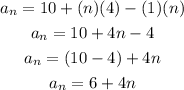
d)

You can find any real situation that something is increasing by 4 each time

Example:

The length of the plant is increasing by 4 cm each day

e)

day: length of the plant

1. 10

2. 14

3. 18

4. 22

f)

To find the number of blocks in figure 31

Substitute n by 31, then find an in the explicit formula

`\begin{gathered} n=31 \\ a_(31)=6+4(31) \\ a_(31)=6+124 \\ a_(31)=130 \end{gathered}`

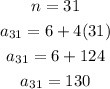
Figure 31 has 130 blocks

g)

To find the number of the figure that has 50 blocks

Substitute an by 50 and find n

`\begin{gathered} a_n=50 \\ 50=6+4n \end{gathered}`

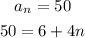
Subtract 6 from both sides

`\begin{gathered} 50-6=6-6+4n \\ 44=4n \end{gathered}`

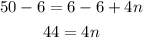
Divide both sides by 4 to find n

`\begin{gathered} (44)/(4)=(4n)/(4) \\ 11=n \end{gathered}`

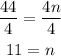
The figure that has 50 blocks is the 11 figure