True or false10. If (1+i) is a root of a quadratic equation with real coefficients, the equation is y=x^2+2x+2

Question

asked Nov 21, 2023 139k views

1 Answer

MikeTP · Answer 1 · 2023-11-25T14:24:33+0000

We know that a root of a quadratic function is a value of x that makes the function equal to 0.

So,

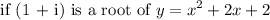
$\begin{gathered} \text{ if (1 + i) is a root of }y=x^2+2x+2 \\ \end{gathered}$

it must be fulfilled that,

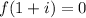
Now, we must replace (1 + i) in the function

$\begin{gathered} (1+i)^2+2(1+i)+2 \\ \\ \\ \end{gathered}$

solving the parentheses,

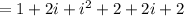
Using that i^2 = -1

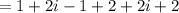
grouping similar terms

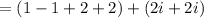
$\begin{gathered} =(1-1+2+2)+(2i+2i) \\ \end{gathered}$

Finally, simplifying

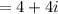
We can see that

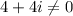
$4+4i\\e0$

So, (1 + i) is not a root of the equation.

The statement is false.