EXPLANATION
Let's see the facts:
Maximum height = 64 feet Time = 2 seconds
Time to hit the ground = 4 seconds
Gravity = 9.8 m/s^2
The position equation is as follows:

Representing this situation:
Time to reach peak=
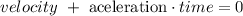
Replacing terms:
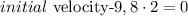
Isolating the initial velocity:
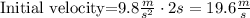
Now, we now that at first segment, the ball travel 64 feet to the maximum height, thus we have a height of 64 feet. Now, we need to compute the distance to the ground applying the free fall kinematic equation.
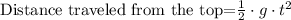
As the time elapsed from the top was 4 seconds, the equation would be:
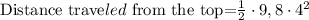
Multiplying numbers and computing the powers:
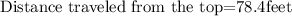
Now, we need to subtract the distance traveled from the top to the maximum height reached in order to obtain the height:

Replacing terms:
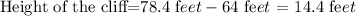
The cliff is 14.4 feet tall