To answer this question, we can proceed as follows:
1. We know that the area of a rectangle is given by:
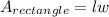
2. And we have that:
• The ,length, is 5ft more than its width ---> x + 5.
,
• The ,width, is x.
,
• The ,area of the garden, is 336 square feet.
3. Now, we have that:
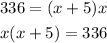
4. We have to multiply the terms on the left side of the equation as follows:
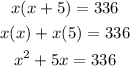
5. Now we need to subtract 336 from both sides of the equation:
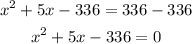
6. We have a quadratic equation, and we can solve it using the quadratic formula as follows:
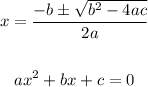
7. From the resulting quadratic function, we have:
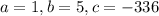
Then, we have:
![\begin{gathered} x=(-b\pm√(b^2-4ac))/(2a) \\ \\ x=\frac{-5\operatorname{\pm}√(5^2-4(1)(-336))}{2(1)} \\ \\ x=(-5\pm√(25+1344))/(2) \\ \\ x=(-5\pm√(1369))/(2) \\ \\ x=(-5\pm37)/(2) \end{gathered}]()
8. From the answer, we have two possible solutions here:
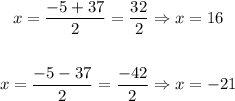
9. Since the value of x = -21 is meaningless to this answer - the values for length or width cannot be negative, then the value for x = 16.
10. Now, to find the values for the width and the length, we have:
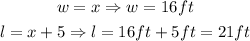
In summary, we have that:
The width of the garden is 16ft, and the length of the garden is 21ft.