As per given by the question,
(a) There are given that diameter of the ice cream cone is 3.5 cm, and height is 6 cm.
Now,
Ftom the formula of the volume of the ce cream.
So,
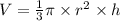
Then,
There are given tha a diameter is 3.5,
So, Radius of the ice cream cone is,
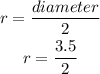
Now,
Substitute the value in above formula,
So,
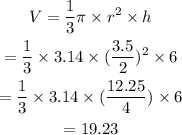
Hence, the 19.23 cm ice cream fit in the cone.
(b). There are given that diameter of 1 scoop ice cream is 3.5 cm.
Then,
The formula of the one scoop ice cream is,
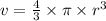
Now,
The radius is,
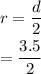
So,
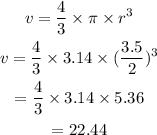
Hence, the volume of the one scoop ice cream is 22.44 cm.