Given the side lengths of a triangle:
8, 10 and 15.
Let's apply the pythagorean theorem to classify the triangle.
We have:
If a²+b² = c² then it's a right triangle
If a²+b² > c² then it's an acute triangle
If a²+b² < c² then it's an obtuse triangle.
Where:
a = 8
b = 10
c = 15
Thus, we have:
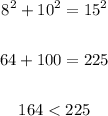
Since a²+b² < c², the triangle is an obtuse triangle.
ANSWER:
Obtuse