Question

For for each quadratic function below use method of completing the Square or averaging the x-intercept to write the equation in the Graphing form. then, State Line of symmetry and give the vertex of each parabola. try to use the method at least one.
`a.f(x) = {x}^(2) + 6 x + 15`
`b.y = {x}^(2) - 4x +9`
`c.f(x) = {x}^(2) - 8x`
`d.y = {x}^(2) + 7x - 2`

Answer 1

We have the expressions:

`f(x)=x^2+6x+15`
`y=x^2-4x+9`
`f(x)=x^2-8x`
`y=x^2+7x-2`

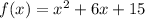
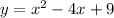
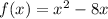
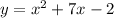
Now, with this we operate as follows:

a)

`f(x)=x^2+6x+15=x^2+6x+9+15-9`
`\Rightarrow(x+3)^2+6`

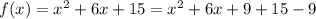
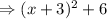
Then, the axis is x = -3 and the vertex (-3, 6)

b)

`y=x^2-4x+9=x^2-4x+4+9-4`
`\Rightarrow(x-2)^2+5`

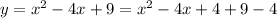
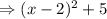
Then, the vertex is (2, 5) and the axis is x = 2.

c)

`f(x)=x^2-8x+4-4\Rightarrow(x-2)^2-4`

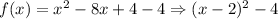
Then, the vertex is (2, -4) andd the axis is x = 2.

d)

`y=x^2+7x-2=x^2+7x+(49)/(4)-2-(49)/(4)`
`\Rightarrow(x+(7)/(2))^2-(57)/(4)`

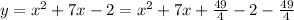
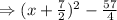
Then, the vertex is (-7/2, -57/4) and the axis is -7/2.