Answer: 0.0397
Step-by-step explanation
Given
• Normal distribution
,
• μ = 25.9
• σ = 74.2
,
• n = 99
,
• Mean between 28.1 and 35.6
Procedure
As we have a normal distribution, we can get Z-score to approximate the probability using the following formula for both values:
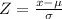
• Lower value
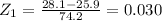
• Upper value
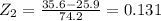
![P\left(28.1Using the Standard Normal Table we can conclude that:[tex]P(28.1\lt M\lt35.6)=P(0.030\lt Z\lt0.131)=0.0397]()