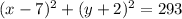Question

Write an equation of the circle centered at (7, -2) that passes through (-10, 0).

Answer 1

Given

The center of the circle is (7,-2).

And, it passes through (-10,0).

To find the equation of the circle.

Step-by-step explanation:

It is given that,

The center of the circle is (7,-2).

And, it passes through (-10,0).

Then, the standard form of the circle is given by,

`\begin{gathered} (x-h)^2+(y-k)^2=r^2 \\ \Rightarrow(x-7)^2+(y+2)^2=r^2\text{ \_\_\_\_\_\_\lparen1\rparen} \end{gathered}`

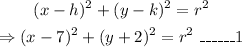
Since it passes through (-10,0).

Then,

`\begin{gathered} (-10-7)^2+(0+2)^2=r^2 \\ 289+4=r^2 \\ r^2=293 \end{gathered}`

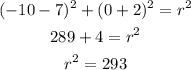
Hence, the equation of the circle is,

`(x-7)^2+(y+2)^2=293`