Given:
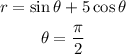
To find: The slope of the tangent line
Step-by-step explanation:
Let us take,
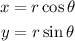
Substituting the r-value in the above equations, we get,
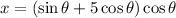
Differentiating using the product rule,
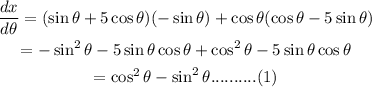
And we have,
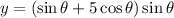
Differentiating using the product rule,
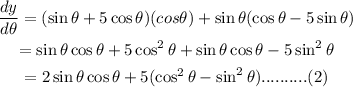
Dividing equation (2) by (1), we get
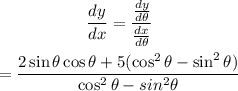
The slope of the tangent line at the given angle is,
![\begin{gathered} [(dy)/(dx)]_{(\pi)/(2)}=(2(1)(0)+5(0-1))/(0-1) \\ =-(5)/(-1) \\ =5 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/x3wsgapnxsobpqmh1pbgzbseeo9x61xluv.png)
Final answer:
The slope of the tangent line to the given polar curve at the point specified by the value of θ is 5.