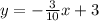Given the points:
(x1, y1) ==> (-50, 18)
(x2, y2) ==> (40, -9)
Take the slope-intercept form:
y = mx + b
Where m is the slope and b is the y-intercept
To write the slope intercept form of the equation, find the slope.
Use the slope formula below:
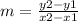
Thus, we have:
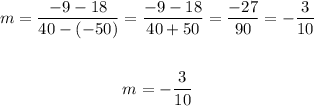
Substitute m for -3/10 in y = mx + b
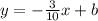
To find the y-intercept, b, use the point (-50, 18).
Substitute -50 for x and 18 for y:

The y-intercept of the equation is 3.
Therefore, the slope intercept form of the equation is:
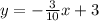
ANSWER: