Question

Hi, how do I find the equation of the line in general form going through points (4,-10) and (-2, -7)

Answer 1

`2y+x+16=0`

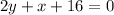
Step-by-step explanation

We want to find the equation of the line in general form i.e.:

`Ax+By+C=0`

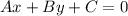
where A, B, C are constants

To do this, we have to first find the slope of the line using the formula:

`m=(y_2-y_1)/(x_2-x_1)`

where (x1, y1) and (x2, y2) are the two points the line passes through.

We have that the two points are (4, -1) and (-2, -7)

Therefore, the slope of the line is:

`\begin{gathered} m=(-7-(-10))/(-2-4) \\ m=(-7+10)/(-2-4) \\ m=(3)/(-6) \\ m=-(1)/(2) \end{gathered}`

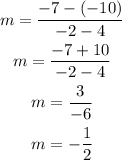
Now, we find the equation of the line in point-slope form by using the formula:

`y-y_1=m(x-x_1)`

Therefore, we have:

`\begin{gathered} y-(-10)=-(1)/(2)(x-4) \\ y+10=-(1)/(2)x+2 \end{gathered}`

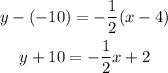
To express it in the general form, first, eliminate the fraction by multiplying both sides of the equation by 2:

`2y+20=-x+4`

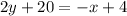
Now, take all the terms to the left side of the equation:

`\begin{gathered} 2y+x+20-4=0 \\ 2y+x+16=0 \end{gathered}`

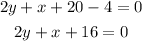
That is the equation of the line in the general form.