Question

write symbolic expression, then get rid of radical and make it exponential expression in fractional form "The eighth root of fifty seven to the sixth degree"

Answer 1

We need to write as an exponential in fractional form the expression:

`\text{ The eighth root of fifty-seven to the sixth degree}`

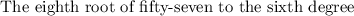
The "eighth root" is represented by the symbol:

`\sqrt[8]{\ldots}`

And the exponential "fifty-seven to the sixth degree" is:

`57^6`

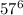
So, the whole expression is written as:

`\sqrt[8]{57^6}`

Now, we need to use the following properties of exponentials:

`\begin{gathered} \sqrt[n]{x}=x^{(1)/(n)} \\ \\ (y^a)^b=y^(a\cdot b) \end{gathered}`

Then, using those properties, we obtain:

`\sqrt[8]{57^6}=(57^6)^{(1)/(8)}=57^{6\cdot(1)/(8)}`

Notice that:

`6\cdot(1)/(8)=(6)/(8)=(6/2)/(8/2)=(3)/(4)`

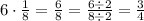
Thus, we obtain:

`\sqrt[8]{57^6}=57^{(3)/(4)}`