Question

quadratic functions. Please help with both i’m just very confused and don’t understand it. i just learned in class today. Find the vertex make a table about use and graph also give the equation of the line of symmetry the maximum or minimum value the domain and range

Answer 1

Check below, please.

10) We were told to find the Vertex, a table of values, and a graph. So let's start out with the vertex. For that, we need a formula:

`\begin{gathered} V(h,k) \\ h=-(b)/(2a) \end{gathered}`

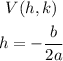
10.2) So let's plug into the h coordinate the given values:

`\begin{gathered} y=-x^2-4x+3 \\ h=(-(-4))/(2(-1))=(4)/(-2)=-2 \\ \end{gathered}`

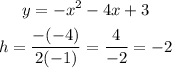
To find the k coordinate, just plug into the quadratic equation the h coordinate:

`\begin{gathered} k=-(-2)^2-4(-2)+3 \\ k=-(4)+8+3 \\ k=-4+8+3 \\ k=4+3 \\ k=7 \\ --- \\ V(-2,7) \end{gathered}`

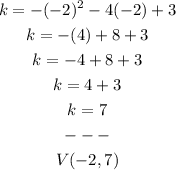
10.3) Now, let's make a table of values, a.k.a t-table:

Note that we pick random values for x, plug them into the function then we get the y-values. So we can pick the following coordinate points:

(-2,7),(-1,6), (0,3), (1,-2), (2, -9)

Note that since the a coefficient is -1 the curve is downward.

10.4) Based on the graph, we can trace the axis of symmetry, i.e. the axis that evenly divides the parabola into two halves. We just need for that, the x-coordinate of the Vertex. So, the axis of symmetry is:

`x=-2`

10.4) The Domain of a quadratic function, i.e. the set of entries, usually is all the values for the Real Set. So we can write out:

`D=(-\infty,\infty)\text{ or D=}\mathfrak{\Re }`

10.5) The Range is the set of the outputs for each entry of the Domain set. Notice that the concavity is down wars, so we can see that the y-coordinate of the vertex k= y=7 is the highest y-value for this function, hence we can state the Range as:

`R=(-\infty,7\rbrack`

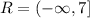
10.6) Since this parabola is open downward then we can state that this parabola has a maximum given by its vertex.