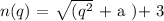
We need to find the values of "a" that result in the function being real. For that the number inside the square roots must be greater or equal to zero, therefore:

We need to isolate the "a" variable on the left side now.
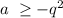
The value of "a" is anything greater or equal to -q².