Part A:
It depends on the signs:
The line is solid if:
The inequality involves a greater equal or a lesser equal.
example:
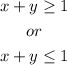
The line is dashed if:
Inequality involves a greater than or less than.
example:
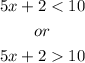
This is because when we speak of a strict greater or lesser. the area does not touch the boundary line. While in the opposite case if it touches the border line.
Part B:
Let's evaluate the point (x,y) = (0,0):
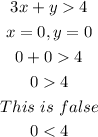
We can conclude that this point is not a solution for the inequality, so, it does not belong to the solution region:
Part C:
Let's focus on graph the equivalent line:
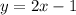
From this equation we can see:

since it is greater than (>), the line is dashed and the shaded region is above the line: