Question

Solve the equation below in the interval from 0 to 2π. Round your answer to the nearest hundredth. cos (πθ) = − 0.6

Answer 1

Trigonometric Equations

Solve:

`cos(\pi\theta)=-0.6`

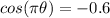
Using the inverse cosine function in the calculator, we get:

`\begin{gathered} \pi\theta=\arccos(-0.6) \\ \\ \pi\theta=2.2143\text{ rad} \end{gathered}`

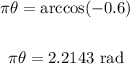
There is another solution in quadrant III

`\begin{gathered} \\ \pi\theta=(2\pi-2.2143)\text{ rad} \\ \\ \pi\theta=4.069\text{ rad} \end{gathered}`

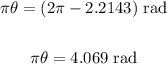
Dividing by π, we get the first two solutions:

`\begin{gathered} \\ \theta=(2.2143)/(\pi)\text{ rad} \\ \\ \theta=0.7048\text{ rad} \end{gathered}`

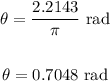
The second solution is:

`\begin{gathered} \theta=(4.069)/(\pi)\text{ rad} \\ \\ \theta=1.2952\text{ rad} \end{gathered}`

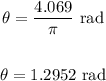
We can find more solutions by adding 2π to the inverse cosine angle.

`\begin{gathered} \pi\theta=(2.2143+2\pi)\text{ rad} \\ \\ \pi\theta=8.4975\text{ rad} \end{gathered}`

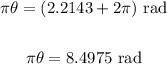
Dividing by π:

`\begin{gathered} \theta=(8.4975)/(\pi)\text{ rad} \\ \\ \theta=2.7078\text{ rad} \end{gathered}`

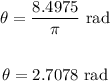
A fourth solution is found as follows:

`\begin{gathered} \pi\theta=(2\pi+4.069)\text{ rad} \\ \\ \theta=(10.3521)/(\pi)\text{ rad} \\ \\ \theta=3.2952\text{ rad} \end{gathered}`

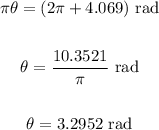
We must keep adding 2π until the solution goes outside of the interval (0, 2π).

`\begin{gathered} \pi\theta=(8.4975+2\pi)\text{ rad} \\ \\ \pi\theta=14.7807\text{ rad} \\ \\ \theta=(14.7807)/(\pi)\text{rad} \\ \\ \theta=4.7048\text{ rad} \end{gathered}`

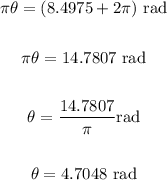
The final solution is found as follows:

`\begin{gathered} \pi\theta=(2\pi+10.3521)\text{ rad} \\ \\ \theta=(16.6353)/(\pi)\text{ rad} \\ \\ \theta=5.2952\text{ rad} \end{gathered}`

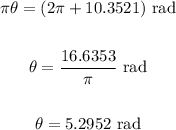
The complete set of solutions is given below:

θ = 0.70 rad

θ = 1.30 rad

θ = 2.70 rad

θ = 3.30 rad

θ = 4.70 rad

θ = 5.30 rad

The next solution would be 4.70 rad but it's greater than 2π, so we stop here