Given:
1-Y=csc x
2-Y=cos x
3-Y=tan x
4-Y=cot x
Required:
To find the functions whose graph has asymptotes located at the values x= ±nπ?
Step-by-step explanation:
To find the vertical asymptotes the denominator of the function should be zero.
In the given functions cosx has no denominator.
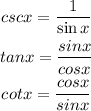
The values of sin function at
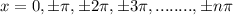
is 0.
The value of cos function at
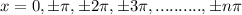
is not 0.
Thus we can observe that the sine function is 0 at the values of
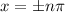
The cscx and the cotx function has denominator sinx.
Thus the functions cscx and cotx graph have asymptotes located at the values x= ±nπ?
Final Answer:
Thus 1 and 4 is the correct answer.