Question

Find the zeros by using the quadratic formula and tell whether the solutions are real or imaginary. F(x)=x^2–10x+30

Answer 1

The solution are imaginary numbers (complex numbers)

`\begin{gathered} x=\frac{10+i\sqrt[]{20}}{2}=5+i\frac{\sqrt[]{20}}{2}=5+2.24i \\ \text{and} \\ x=\frac{10-i\sqrt[]{20}}{2}=5-i\frac{\sqrt[]{20}}{2}=5-2.24i \end{gathered}`

Step-by-step explanation:

Given the quadratic function;

`f(x)=x^2-10x+30`

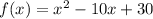
The zeros of the function are at f(x)=0;

`\begin{gathered} f(x)=x^2-10x+30=0 \\ x^2-10x+30=0 \end{gathered}`

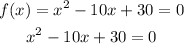
Solving using the quadratic formula;

`x=\frac{-b\pm\sqrt[]{b^2-4ac}_{}}{2a}`

where;

a = 1

b = -10

c = 30

Substituting the values, we have;

`\begin{gathered} x=\frac{-b\pm\sqrt[]{b^2-4ac}_{}}{2a} \\ x=\frac{-(-10)\pm\sqrt[]{(-10)^2-4(1)(30)}_{}}{2(1)} \\ x=\frac{10\pm\sqrt[]{100^{}-120}_{}}{2} \\ x=\frac{10\pm\sqrt[]{-20}_{}}{2} \\ x=\frac{10\pm\sqrt[]{(-1)20}_{}}{2} \\ x=\frac{10\pm\sqrt[]{(i^2)20}_{}}{2} \\ x=\frac{10\pm i\sqrt[]{20}_{}}{2} \end{gathered}`

Recall that;

`-1=i^2`

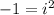
Solving further we have;

`\begin{gathered} x=\frac{10+i\sqrt[]{20}}{2}=5+i\frac{\sqrt[]{20}}{2}=5+2.24i \\ \text{and} \\ x=\frac{10-i\sqrt[]{20}}{2}=5-i\frac{\sqrt[]{20}}{2}=5-2.24i \end{gathered}`

Therefore, the solution are imaginary numbers (complex numbers)